Triangulo equilátero

En geometría, un triángulo equilátero, es un polígono regular con tres lados iguales. En la geometría euclídea tradicional, los triángulos equiláteros también son equiangulares, es decir, los tres ángulos internos también son congruentes entre sí, cada ángulo vale 60°.

construcción 

Todo triángulo equilátero consta de tres lados iguales y tres ángulos congruentes entre sí. Teniendo esto en cuenta, su construcción puede resultar muy sencilla.

Para lograr una congruencia en los lados, es aconsejable trazar el triángulo dentro de una circunferencia (circunscrito), para ello se pueden emplear los siguientes pasos:

• Trazar la circunferencia con el compás.
• Trazar un radio y, a partir de éste, marcar con el transportador un ángulo de 120°.
• Partiendo del trazo anterior, trazar otro ángulo de 120° (puede hacerse nuevamente con el transportador o auxiliándose del compás).
• Unir los puntos.

Una alternativa puede ser la siguiente:

• Teniendo dos puntos unidos en línea recta (A y B).
• Trazar una circunferencia con centro en A con radio igual a la distancia entre A y B.
• Trazar una circunferencia con centro en B con radio igual a la distancia entre A y B.
• Siendo Γ el punto en el que se cortan las dos circunferencias construidas, unir Γ con A y B

propiedades 

Dada cualquier longitud , es posible determinar por medio del Teorema de Pitágoras las siguientes propiedades: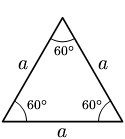

• El valor del área es igual a 
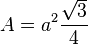
• El valor del perímetro es igual a 
• El radio de un círculo circunscrito es 
• El radio de un círculo inscrito es 
• La altura es .

http://es.wikipedia.org/wiki/Tri%C3%A1ngulo_equil%C3%A1tero