Un triángulo puede ser definido como un polígono de tres lados, o como un polígono con tres vértices.
El triángulo es el polígono más simple y el único que no tiene diagonal. Tres puntos no alineados definen siempre un triángulo (tanto en el plano como en el espacio).
Si se agrega un cuarto punto coplanar y no alineado, se obtiene un cuadrilátero que puede ser dividido en triángulos como el de la figura de la izquierda. En cambio, si el cuarto punto agregado es no coplanar y no alineado, se obtiene un tetraedro que es el poliedro más simple y está conformado por 4 caras triángulares.
Todo polígono puede ser dividido en un número finito de triángulos, esto se logra por triangulación. El número mínimo de triángulos necesarios para esta división es n-2, donde n es el número de lados del polígono. El estudio de los triángulos es fundamental para el estudio de otros polígonos, por ejemplo para la demostración del Teorema de Pick.
En geometría euclidiana la suma de los tres ángulos internos de un triángulo es siempre 180°, lo que equivale a π radianes:
Esta propiedad es el resultado de la geometría euclidiana. No se verifica en general en la geometría no euclidiana.
Euclides había demostrado este resultado en sus Elementos (proposición I-32) de la siguiente manera: se traza una paralela a la línea (AB) que pasa por C. Siendo paralelas, esta recta y la recta (AB) forman con la recta (AC) ángulos iguales, codificados en color rojo en la figura de la derecha (ángulos alternos-internos). Del mismo modo, los ángulos codificados en color azul son iguales (ángulos correspondientes). Por otro lado, la suma de los tres ángulos del vértice C es el ángulo llano. Así que la suma de las medidas del ángulo de color rojo, del ángulo verde y del azul es un ángulo de 180° (o π radianes). En conclusión, la suma de los ángulos de un triángulo es 180°.
Otras propiedades
- La suma de las longitudes de dos de los lados de un triángulo es siempre mayor que la longitud del tercer lado.
- El valor de la paralela media de un triángulo (recta que une dos puntos medios de dos lados) es igual a la mitad del lado paralelo.
- Los triángulos (polígonos de tres lados) son los únicos polígonos siempre convexos, no pueden ser cóncavos, dado que ninguno de sus tres ángulos puede superar los 180 grados o
 radianes.
radianes.
- Para cualquier triángulo se verifica el Teorema del seno que establece: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos
 Para cualquier triángulo se verifica el Teorema del coseno que establece: «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:
Para cualquier triángulo se verifica el Teorema del coseno que establece: «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:
- Para cualquier triángulo rectángulo, cuyos catetos miden a y b, y cuya hipotenusa mida c, se verifica el Teorema de Pitágoras:
De la ecuación anterior se deducen fácilmente 3 fórmulas de aplicación práctica:
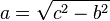 |  | 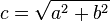 |



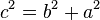
No hay comentarios.:
Publicar un comentario