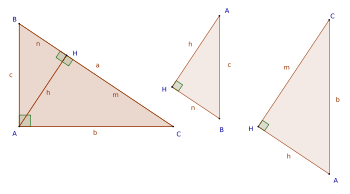
Mundo de las matematicas: marzo 2015

Resolución de triangulo rectángulo

1 Se conocen la hipotenusa y un cateto:

Ejemplo:

Resolver el triángulo conociendo:

a = 415 m y b = 280 m.

sen B = 280/415 = 0.6747 B = arc sen 0.6747 = 42° 25′

C = 90° - 42° 25′ = 47° 35′

c = a cos B c = 415 · 0.7381 = 306. 31 m

2 Se conocen los dos catetos:

Ejemplo:

Resolver el triángulo conociendo:

b = 33 m y c = 21 m .

tg B = 33/21 = 1.5714 B = 57° 32′

C = 90° − 57° 32′ = 32° 28′

a = b/sen B a = 33/0.8347 = 39.12 m

3 Se conocen la hipotenusa y un ángulo agudo:

Ejemplo:

Resolver el triángulo conociendo:

a = 45 m y B = 22°.

C = 90° - 22° = 68°

b = a sen 22° b = 45 · 0.3746 = 16.85 m

c = a cos 22° c = 45 · 0.9272 = 41.72 m

4 Se conocen un cateto y un ángulo agudo:

Ejemplo:

Resolver el triángulo conociendo:

b = 5.2 m y B = 37º

C = 90° - 37° = 53º

a = b/sen B a = 5.2/0.6018 = 8.64 m

c = b · cotg B c = 5.2 · 1.3270 = 6. 9 m

http://www.vitutor.com/al/trigo/tri_12.html

Angulos notable de las razones trigonométrica

Razones trigonométricas de 30º y 60º

La altura divide al triángulo equilátero en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 60º y 30º.

Si aplicamos el teorema de Pitágoras obetenemos la altura en función del lado:

Razones trigonométricas de 45º

La diagonal divide al cuadrado en dos triángulos rectángulos iguales cuyos ángulos miden 90º, 45º y 45º.

Si aplicamos el teorema de Pitágoras obetenemos la diagonal en función del lado:

Razones trigonométricas de ángulos notables

www.aritor.com/trigonometria/angulos_notables.html

Funciones o razones trigonométrica

Se las conoce de las dos maneras, a tal punto que el nombre es correcto en ambos casos: hablar de razones o funciones trigonométricas es lo mismo y hacemos referencia a las relaciones que podemos establecer entre los lados y los ángulos de un triángulo rectángulo.

elementos y notacion triángulo rectangulo

elementos y notacion triángulo rectangulo

Llamamos a los vértices con las letras mayúsculas A, B y C, siendo siempre A el ángulo recto que hemos destacado en color rojo.

En cuando a los lados, los llamamos según sean opuestos a los ángulos siempre con las mismas letras que éstos, pero minúsculas; de ese modo la hipotenusa será siempre a y los catetos respectivos serán b y c.

Es importante que comprendas el concepto de cateto opuesto y cateto adyacente, porque forman parte de las funciones que estudiamos en este post. Para que tú definas un cateto como opuesto o adyacente, ten en cuenta que lo es respecto a un ángulo. Es decir, primero eliges en un ángulo y luego, el cateto que esté enfrentado con él será el opuesto y el que está a su costado (es decir que el lado forma parte del ángulo) será el adyacente.

Mira la imagen con atención, y observa que hemos marcado en verde un ángulo y una flecha te muestra cuál es el cateto que está frente a él; ese será el cateto opuesto y el adyacente el que está a su costado.

Tiene que quedarte claro que cuando hables del otro ángulo, los roles entre los catetos cambiarán. La hipotenusa, es una sola y es el lado que se opone al ángulo recto.

Las razones o funciones trigonométricas que pueden establecerse para cualquier triángulo rectángulo son seis y se dividen en dos grupos:

Razones o funciones fundamentales
Razones o funciones recíprocas

Entre ellas, al principio sólo trabajaremos con las fundamentales.

Vale la aclaración: cuando se habla de cateto opuesto (c op), cateto adyacente (c ady) y de hipotenusa (hip) en las fórmulas que anteceden, siempre se quiere decir “medida de“, es decir por ejemplo: medida del cateto opuesto dividido medida de la hipotenusa. Sólo se abrevian de ese modo para memorizarlas de un modo mas sencillo, pero en todos los casos, hablamos de las medidas de esos lados.

Las funciones recíprocas también son tres. Aunque no las utilizaremos al principio, es importante saber que existen y cuáles son. Se llaman respectivamente: cosecante (es la inversa a la función seno, es decir hip/c op), secante (es la inversa a la función coseno, es decir hip/c ady) y cotangente (es a inversa a la función tangente, es decir c ady / c op).

Triangulo rectángulo y sus propiedades

En geometría, se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90 grados. Las razones entre las longitudes de los lados de un triángulo rectángulo es un enfoque de la trigonometría plana. En particular, en un triángulo rectángulo, se cumple el llamado teorema de Pitágoras ya conocido por los babilonios.

propiedades

Todo triángulo rectángulo tiene dos ángulos agudos.
La hipotenusa es mayor que cualquiera de los catetos.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
La suma de la hipotenusa y el diámetro de un círculo inscrito en el triángulo es igual a la suma de los catetos.
Para efectos de área, un cateto cualquiera se puede considerar como base y el otro cateto como altura.

relaciones métricas

Las relaciones métricas del triángulo rectángulo son cuatro. Los tres triángulos formados al trazar la altura relativa a la hipotenusa son rectángulos y semejantes.